Spaces, Vectors and Coordinates
Learn the fundamentals of coordinate systems and vectors to create spatial representations
In this lesson, we'll cover coordinate systems and vectors, which form the basis of spatial representation in computer graphics. These mathematical constructs allow us to specify the positions of objects in our virtual worlds.
We'll start by defining spaces and the Cartesian coordinate system. Then, we'll examine vectors as a way to store positional data using multiple components. Finally, we'll explore how to implement these structures in C++ and understand the transformations required to convert between different coordinate spaces.
These concepts serve as building blocks for all spatial calculations in game development, from simple 2D positioning to complex 3D transformations.
Spaces
We can think of virtual worlds as spaces. In maths and physics, a space contains a collection of objects that obey pre-defined structures and rules. Typically, the structure and rules we want to implement mirror those we are most familiar with in the real world.
That means we will be interested in things like the distance between objects, and rules that govern how objects can move around the space.
The most basic object that exists within spaces is a point. We can model more complex objects by creating a collection of such points - for example, a triangle could be defined by 3 points - one for each of its corners. A full 3D monster, created by an artist, could have thousands of points to define its shape.
The most important property we care about when it comes to these points is what their current position is within the space. We can implement the concept of position by imagining our space as a grid.
For now, we will work with a two-dimensional space, which we'll represent visually as a grid:

Coordinate Systems
To communicate where objects are positioned and how they move within a space, we need to introduce a coordinate system. The most useful system is the Cartesian coordinate system.
We can set up this system by placing an axis along each dimension so that, for a two-dimensional space, we'd have two dimensions. Conventionally, we call the horizontal axis the axis, and the vertical axis the axis.

With the axes set up, we can now define each point by a collection of numbers - one for each dimension the space has. In a two-dimensional space, each point will have two values - one for its position along the axis, and one for its position along .
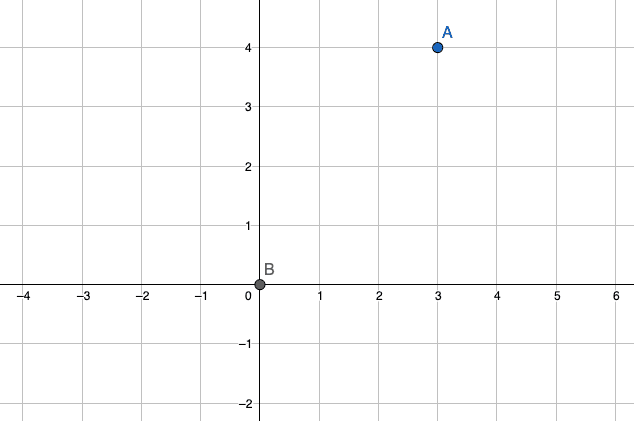
The Origin
In a cartesian coordinate system, the point where all the axes intersect is referred to as the origin and can generally be considered the center of the space.
In the previous example, point is at the origin of our space. The origin of a space is also sometimes denoted by the letter .
Components and Vectors
The position of any point in a space will have several components - one component for each dimension in the space. Each component will represent the point's position along that dimension.
In the above example, we're working in a two-dimensional space, so each position will have two components. Point 's component is as its horizontal position is units in the positive direction from the origin. Its component is as its vertical position is units in the positive direction from the origin.
A position in a space is often represented using a vector, which is simply an ordered list of numbers. Mathematically, vectors are often written as a collection of comma-separated values within brackets. So, for example, .
The components of a vector are normally denoted using subscript notation. For example, and . We could also denote them as and if preferred - we can choose whatever format we think is best for the idea we're trying to communicate.
Components and Vectors in C++
In C++, we represent mathematical vectors using custom data structures. A common approach is to define a struct that contains the vector's components as member variables. Let's implement a two-dimensional vector type called Vec2:
// Vec2.h
#pragma once
struct Vec2 {
float x;
float y;
};This simple struct allows us to store both the x and y components of a vector in a single object. To use our Vec2 type, we can create instances and access their components using the dot operator (.):
// main.cpp
#include <iostream>
#include "Vec2.h"
int main() {
// Create a vector to represent position (3,4)
Vec2 A{3.0, 4.0};
// Access and display the components
std::cout << "Ax = " << A.x
<< ", Ay = " << A.y;
// We can also modify components individually
A.x = 5.0;
std::cout << "\nNew Ax = " << A.x;
}Ax = 3.0, Ay = 4.0
New Ax = 5.0As we progress, we'll extend this Vec2 struct with additional functionality to perform vector operations like addition, subtraction, scaling, and calculating distances.
Transformations
When we're defining a space, we are free to use any coordinate system we want, and we can position the origin in any location. The coordinate system we introduced above is a common convention and is likely to be familiar. We should note that it has the following characteristics:
- The axis is horizontal and increasing values corresponds to moving points right
- The axis is vertical and increasing values corresponds to moving points up
- The origin is usually visualized as being in the "center" of the space. We can have a point to the left or the origin by using a negative component, or below the origin by using a negative component.
But these characteristics are not true of every space. For example, we've already seen how SDL typically uses a different system when we're working with windows and surfaces. It also uses the convention of being the horizontal axis and being vertical, but has two main differences:
- Increasing values correspond to moving points down
- The origin is visualized as being at the top-left of the space. As such, components are rarely negative.
The following diagram visualizes the space typically used by SDL:
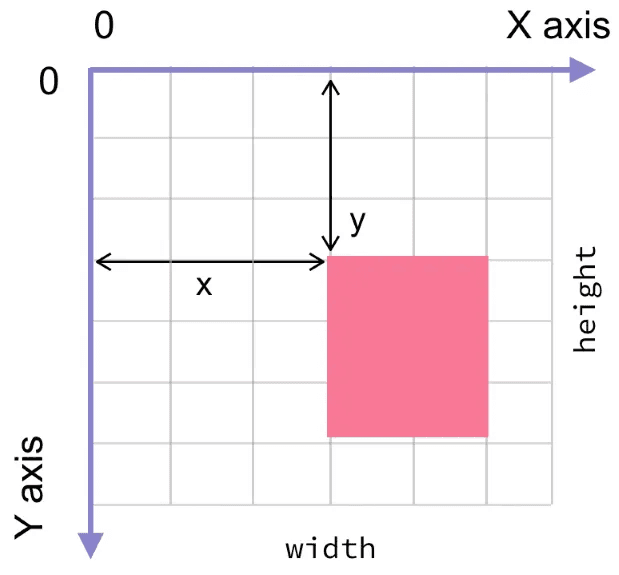
Image Source: Oleg Varaksin
In complex projects, we will typically be dealing with many spaces, each one defined differently. Much of computer graphics involves taking a set of points that are defined in one space and figuring out how they should be defined within some other space.
That other space may have a different origin, different coordinate system, and maybe even a different number of dimensions.
These calculations between spaces are typically referred to as transformations. The following steps outline just some of the main transformations involved in rendering content:
- Local Space: For example, a 3D model is created by an artist working in a content creation tool. It is created in isolation, so the points of the model (vertices) are positioned in a space where the origin may simply be the center of the model.
- World Space: The model is loaded into a level. The vertices of that model now need to be transformed to reflect where that model was positioned within the larger 3D world. At a minimum, the world will have a different origin, but the model may also have been rotated and scaled up or down within our level.
- View Space: The world is viewed from a certain perspective, like a virtual camera. This might be based on where the player's character is within the world, and the direction they are facing. All of our vertices now need to be transformed into this space so they appear in the correct position with respect to the virtual camera's location and rotation.
- Screen Space: The player is viewing this world through their monitor - a two-dimensional grid with its own coordinate system. The points from the view space need to be transformed so objects appear on the correct pixels on the player's screen.
A typical video game scene can have millions of vectors that need to be processed through this transformation pipeline every frame. This is only possible to do in real-time because of our systems' graphics processing units. GPUs are dedicated pieces of hardware designed to perform these specific types of calculations as efficiently as possible.
Summary
In this lesson, we've explored the fundamental mathematical concepts that underpin computer graphics and game development. We've learned how to define spaces using coordinate systems, represent positions as vectors, and understand the various transformations applied when rendering a scene.
These concepts form the foundation upon which we'll build more complex game systems in future lessons. Key takeaways:
- Spaces are mathematical constructs that contain objects with defined structures and rules
- Coordinate systems like the Cartesian system allow us to define positions within a space
- Vectors are ordered lists of numbers that represent positions or other values with magnitude and direction
- In C++, we can implement vectors using custom structs with component members
- Different spaces may use different coordinate systems and origins
- Transformations convert positions between different coordinate systems
- Graphics rendering involves multiple transformations from local space to screen space
Angles and Distance
Learn key geometry concepts like angles, triangles, and vectors to implement distance calculations.