Data Structures and Algorithms

In the previous lesson, we introduced the concept of algorithm complexity, and "Big O" notation for categorizing different algorithms.

One of the example problems we used was creating an algorithm to determine if an array, such as a std::vector, contained any duplicate objects.

We saw we could solve it using the following algorithm, which has a quadratic run time, that is $O(n^2)$:

1bool HasDuplicate(std::vector<int>& Input) {
2  for (size_t i{0}; i < Input.size(); ++i) {
3    for (size_t j{0}; j < Input.size(); ++j) {
4      if (Input[i] == Input[j] && i != j) {
5        return true;
6      }
7    }
8  }
9  return false;
10}

In this lesson, we’ll introduce some techniques for writing better algorithms. A large component of this is creating data structures that are appropriate for the problems we’re trying to solve.

Data Structures and their Performance Characteristics

So far, the main data structure we’ve been using has been the array - either through std::array or std::vector. Arrays store their objects in large, contiguous blocks of memory.

Each object is adjacent to its neighbors - that is, the object at MyArray[3] is right next to the object at MyArray[4].

This approach gives arrays some advantages:

• Iterating over every object in the array is very easy
• We can jump to any object by index, using the [] operator

But it also gives them some limitations:

• Inserting a new object at the start of the array is expensive as, to maintain the contiguous structure, every other object in the array needs to move to make space - an $O(n)$ process
• We can’t easily check if an array contains a specific value. As we saw above, our only approach is to iterate over the array and check every object in turn - an $O(n)$ process

Naturally, arrays are not the only data structures. There are other options we can use, and those options can be optimized for different operations.

Pointer Arithmetic

The ability of arrays to provide fast, constant-time access to any element using the [] operator is directly linked to their contiguous memory storage.

Classes that implement arrays, such as std::vector and std::array, understand three key aspects:

1. Starting Memory Address: The location in memory where their collection begins.
2. Element Size: The size of each element in the array, which is based on the type of object the array stores.
3. Contiguous Storage: The fact that all elements are stored next to each other in memory.

These aspects enable the use of pointer arithmetic to quickly calculate the memory address of any element in the array.

Simplified Example

We’ll implement pointer arithmetic from scratch later in the course. For now, let's consider a simplified example to illustrate how the concept works:

• Suppose we have a std::vector<int> named MyArray.
• Assume int occupies 4 bytes of memory.
• Imagine that MyArray starts at a memory address, say 200.

When we request an element at a specific index, like MyArray[100], the calculation to find its address is straightforward.

Since we know each int is 4 bytes and the elements are stored contiguously, the 100th element (at index 99, as arrays are 0-indexed).

The memory address of MyArray[100] is calculated as $200+(4*100) = 600$

This calculation doesn’t doesn’t increase in complexity as our array gets larger. This allows for constant-time access, denoted as $O(1)$, to any element.

Hash Sets

An alternative way we can store a collection is in a data structure called a hash set, or sometimes simply set.

Unlike an array, sets do not allow us to iterate over them. Rather, they are designed to optimize inserting and searching for objects, both of which can be done in constant time - $O(1)$

The standard library’s implementation of a hash set is std::unordered_set, which we cover in a dedicated lesson later.

Hash Sets using std::unordered_set

This lesson provides a thorough understanding of std::unordered_set, from basic initialization to handling custom types and collisions

For now, we can note that our earlier algorithm can be improved from $O(n^2)$ to $O(n)$ by incorporating a hash set. Rather than using a nested loop to find if our array contains a specific number, we can instead keep track of the numbers we’ve already seen by adding them to a hash set.

Then, for each number in our array, we can check if it’s one we’ve already seen, by checking if our hash set contains it:

1#include <vector>
2#include <unordered_set>
3
4bool HasDuplicate(std::vector<int>& Input) {
5  std::unordered_set<int> PreviousNumbers;
6  for (int i : Input) {
7    if (PreviousNumbers.contains(i)) {
8      return true;
9    } else {
10      PreviousNumbers.emplace(i);
11    }
12  }
13
14  return false;
15}

1bool HasDuplicate(std::vector<int>& Input) {
2  std::unordered_set<int> Set;
3  Set.insert_range(Input);
4  return Set.size() < Input.size();
5}

Linked Lists

Unlike arrays, linked lists can store their elements anywhere in memory - they are not restricted to using a contiguous block:

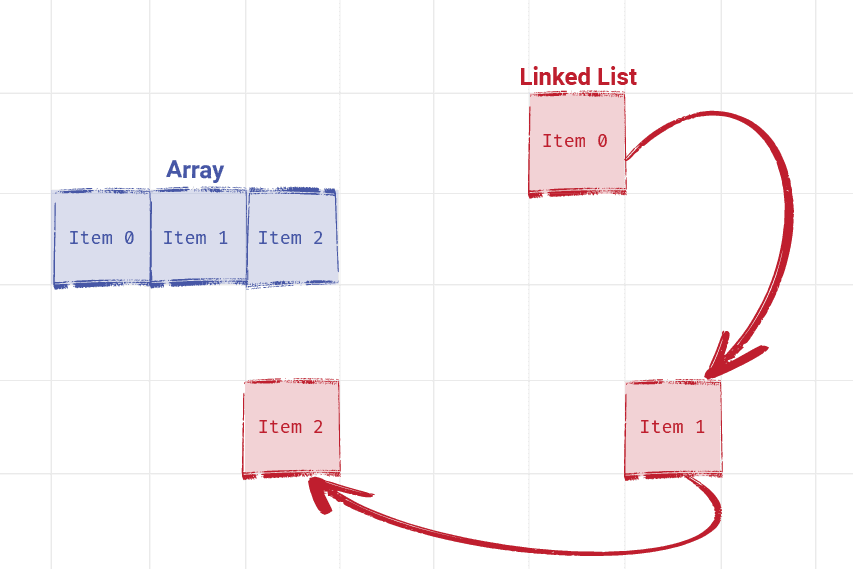
Again, this different approach creates different performance characteristics. Compared to arrays, linked lists lose the ability to jump to arbitrary objects using the [] operator.

We maintain the ability to iterate through a linked list - we just follow the links (pointers) as they guide us through the collection.

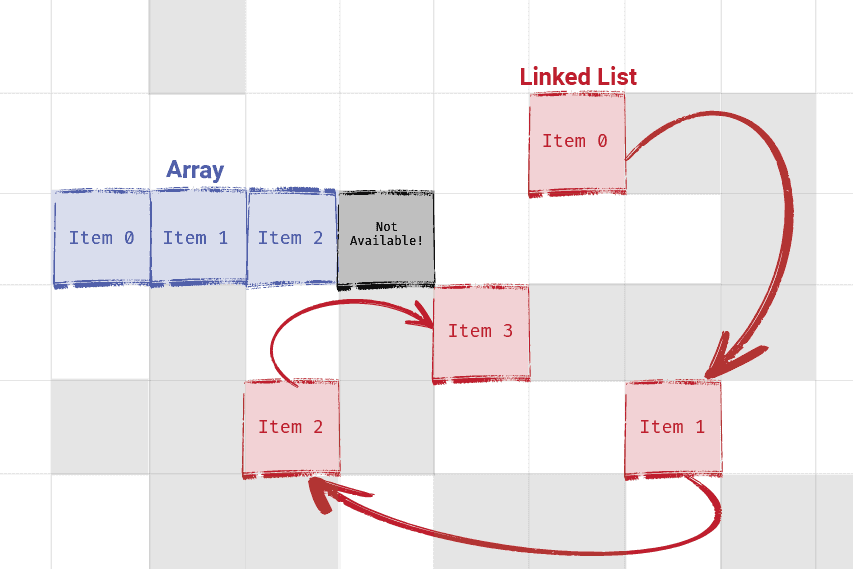
However, their less restrictive memory layout of linked lists means adding and removing objects tends to be faster.

When we remove or add elements to a linked list, none of the other elements need to be moved. Instead, we just need to update the link from the previous element to point to our new addition.

Additionally, unlike arrays, linked lists don’t run out of space - they don’t need to move to a completely different area of memory once they get too big.

Implementing a Linked List

We’ll introduce the standard library’s implementation of a linked list - called std::forward_list - later in this chapter.

However, it’s worth quickly reflecting on how we might implement the key mechanisms of a linked list ourselves. It’s a good review of some key topics, and tasks like implementing and manipulating linked lists from scratch are very commonly asked in technical interviews.

Creating Nodes

With a linked list for storing integers, for example, we are not just storing an integer in each position. Instead, we need to store both the integer, as well as the link to the next item in the collection.

This container, which has both the item we’re storing, as well as a pointer to the next item, is often called a node. It could look something like this:

1struct Node {
2  int Value;
3  Node* Next;
4};

Now, we can create a linked list of three integers using this type. Our linked list can be represented simply by the first node it contains. The end of the linked list is a node with no Next pointer:

1Node Third { 30, nullptr }; // End
2Node Second { 20, &Third };
3Node First { 10, &Second }; // Start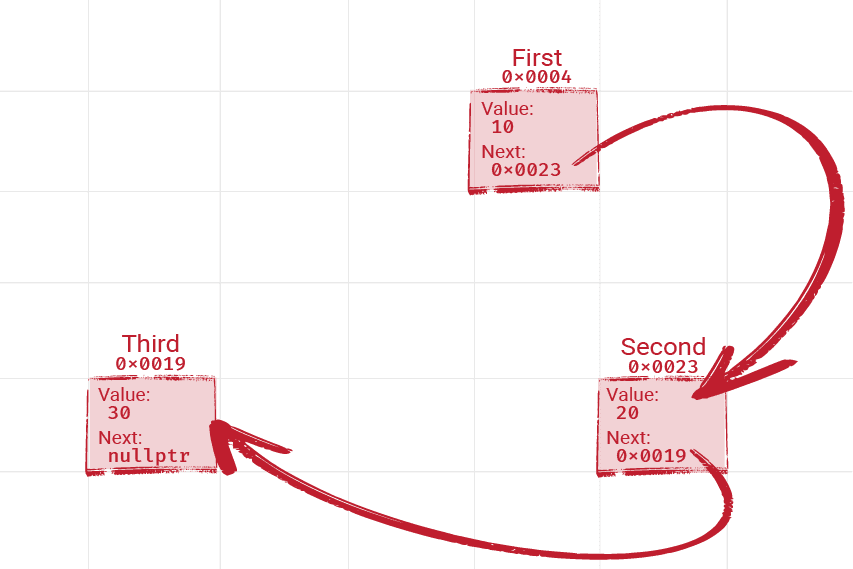

We could use templating here, so our Nodes can store any type of data, not just integers:

1template<typename T>
2struct Node {
3  T Value;
4  Node<T>* Next;
5};

1Node<int> Third { 30, nullptr };
2Node<int> Second { 20, &Third };
3Node<int> First { 10, &Second };

Iterating over a Linked List

To iterate through a linked list, we would follow the pointer within each node, until we encounter the end of the list.

We know we’ve reached the end when the current node’s Next pointer is a nullptr.

Below, our Iterate function uses a recursive approach, where our Iterate function calls itself.

1#include <iostream>
2
Unchanged Code|Show
3struct Node {/*...*/}
9
10void Iterate(auto* Node) {
11  if (Node) {
12    std::cout << Node->Value << ", ";
13    Iterate(Node->Next);
14  }
15}
16
17int main() {
18  Node<int> Third{30, nullptr};
19  Node<int> Second{20, &Third};
20  Node<int> First{10, &Second};
21
22  Iterate(&First);
23}

If our Node is defined, we log its value and call Iterate() passing a pointer to the next node in the list.

Eventually, Iterate will be called with a nullptr, causing the if condition to be false, and the recursion to stop. As such, our previous program iterates through every node in our linked list:

110, 20, 30,

Recursion can be quite difficult to understand, so don’t worry if the previous example doesn’t make sense. We cover recursion in more detail later in the course.

Recursion and Memoization

An introduction to recursive functions, their use cases, and how to optimize their performance

Inserting a Node into a Linked List

To add a new node to our linked list, we need to know the position in which to insert it. Below, this is implemented by the caller to Insert providing a pointer to the node that will come before our new node.

We then perform two actions:

1. We create our new node such that it copies the Next pointer from the previous node
2. We update the previous node’s Next pointer to point to our new node

1#include <iostream>
2
Unchanged Code|Show
3struct Node {/*...*/}
9
Unchanged Code|Show
10void Iterate(auto* Node) {/*...*/}
17
18template <typename T>
19void Insert(Node<T>* Previous, T Value) {
20  auto NewNode = new Node<T>{
21    Value, Previous->Next};// 1 
22
23  Previous->Next = NewNode;// 2 
24}
25
26int main() {
27  Node<int> Third{30, nullptr};
28  Node<int> Second{20, &Third};
29  Node<int> First{10, &Second};
30
31  // Insert a new node after the First node
32  // The new node's value should be 15
33  Insert(&First, 15);
34  Iterate(&First);
35}

Combined, these two actions ensure our new node is inserted into the correct position, and that the integrity of our list is maintained. Our Iterate call shows our updated list:

110, 15, 20, 30,

From here, we can continue to build out our linked list functionality as needed. We might want to add ways to remove nodes, reset the list, and more.

If we were making a linked list implementation that we were going to use, we’d naturally want to encapsulate all this functionality into a custom type, making it easy and safe for other developers to use.

But, the standard library has already done this for us, in the form of std::forward_list. We’ll introduce this later in the chapter.

Summary

In this lesson, we explored the concept of data structures, introducing a few different examples from the C++ standard library. By using the most appropriate data structures, or combining data structures, we can create efficient solutions to the specific problems we’re trying to solve.

Key Takeaways

• Different data structures have different performance characteristics - each has its advantages and disadvantages.
• Arrays store elements in contiguous memory blocks, offering easy iteration and fast access by index, but have limitations in dynamic insertion and element checking.
• Hash sets, particularly std::unordered_set, optimize for quick insertion and searching, enabling operations like checking for duplicates more efficiently.
• Linked lists, with their non-contiguous memory allocation, allow for flexible insertion and deletion of elements without reallocating the entire structure.
• The concept of pointer arithmetic is crucial for understanding how arrays provide fast access to elements, contrasting with the sequential access method in linked lists.
• Real-world performance considerations can sometimes differ from theoretical predictions, emphasizing the importance of choosing the right data structure based on practical testing.

Next Lesson

Iterators

This lesson provides an in-depth look at iterators in C++, covering different types like forward, bidirectional, and random access iterators, and their practical uses.

ContinueView Course