Recursion and Memoization

The basic idea of recursion is a function that calls itself. This is a simple idea, but is particularly common, as it’s a useful way to solve problems that can be broken down into one or more similar, but smaller problems.

This typically comes up in technical interviews for software engineers applying for competitive software engineering positions. A typical process involves:

• Introducing a problem that is best solved by recursion, to determine if a candidate is familiar with the concept
• Solving the problem with recursion in the programming language of choice
• Understanding the performance characteristics and low-level behavior of recursion
• Using caching and memoization techniques to mitigate any performance bottlenecks

This lesson will cover all of these steps, using C++.

Recursive Functions

The most basic example of a recursive function is this:

1void Function(){
2  Function();
3}

The main use case for recursion is when we encounter a problem that can be broken down into one or more similar, but smaller problems.

This function will behave somewhat similarly to an infinite loop. It will load copies of itself onto the stack until the stack runs out of memory and terminates our program.

That’s not especially useful, so a recursive function generally has two parts:

• One or more "base cases", which will end the recursion if true, usually via a return statement
• The remainder of the function body moves the state closer to the base case, and then recursively calls itself

In this example, we show a function that prints a countdown, using a recursive design:

1#include <iostream>
2
3void Countdown(int x){
4  // Base Case
5  if (x <= 0) return;
6
7  // Recursive Case
8  std::cout << x << ", ";
9  Countdown(x - 1);
10}
11
12int main(){ Countdown(5); }

15, 4, 3, 2, 1,

Use Case: Fibonacci Numbers

Fibonacci numbers are a sequence of integers that have many applications in maths and computer science. They are also closely related to the golden ratio, a phenomenon that is frequently observed in nature. More information is available on Wikipedia

The first two Fibonacci numbers are the same: 1 and 1. From there, each subsequent number is generated by adding the previous two. So, the first 8 numbers in the sequence are: 1, 1, 2, 3, 5, 8, 13, 21

Generating a Fibonacci number is a problem that falls into the domain where recursion is useful. This is because the problem can be solved by solving two similar, but smaller problems.

For example, to generate the 10th Fibonacci number, we calculate the 9th and 8th numbers and then add them together.

1Fibonacci(10) == Fibonacci(9) + Fibonacci(8)

More generally:

1Fibonacci(n) == Fibonacci(n-1) + Fibonacci(n-2)

We can implement it in C++ like this:

1#include <iostream>
2
3int Fibonacci(int n) {
4  // Base Cases
5  if (n == 1) return 1;
6  if (n == 2) return 1;
7
8  // Recursive Case
9  return (Fibonacci(n - 1) + Fibonacci(n - 2));  
10}
11
12int main() {
13  std::cout << "10th Fibonacci Number: "
14    << Fibonacci(10);
15}

110th Fibonacci Number: 55

Performance and Branching Recursion

When working with recursion, we should be mindful of performance considerations. This is particularly true when our function is making multiple recursive calls, as in the previous Fibonacci example.

Let's modify our example to see how many calls we’re making:

1#include <iostream>
2
3int Calls{0};
4
5int Fibonacci(int n){
6  ++Calls;
7  if (n == 1) return 1;
8  if (n == 2) return 1;
9  return (Fibonacci(n - 1) + Fibonacci(n - 2));
10}
11
12int main(){
13  std::cout << "10th Fibonacci Number: "
14    << Fibonacci(10);
15
16  std::cout << "\nCalls: " << Calls;
17}

Perhaps surprisingly, calculating the 10th Fibonacci number using this technique requires 109 calls to our function.

110th Fibonacci Number: 55
2Calls: 109

Calculating the 20th Fibonacci number requires 13,529 calls. Calculating the 40th requires 205 million calls, which causes a noticeable delay whilst our computer works it out.

Algorithm Analysis and Big O Notation

An introduction to algorithms - the foundations of computer science. Learn how to design, analyze, and compare them.

To understand why this algorithm requires so much work, let's consider our call to Fibonacci(40). It’s going to call Fibonacci(39) and Fibonacci(38).

We now have two branches of our recursion, the one created by the call to Fibonacci(39) and the one starting at Fibonacci(38)

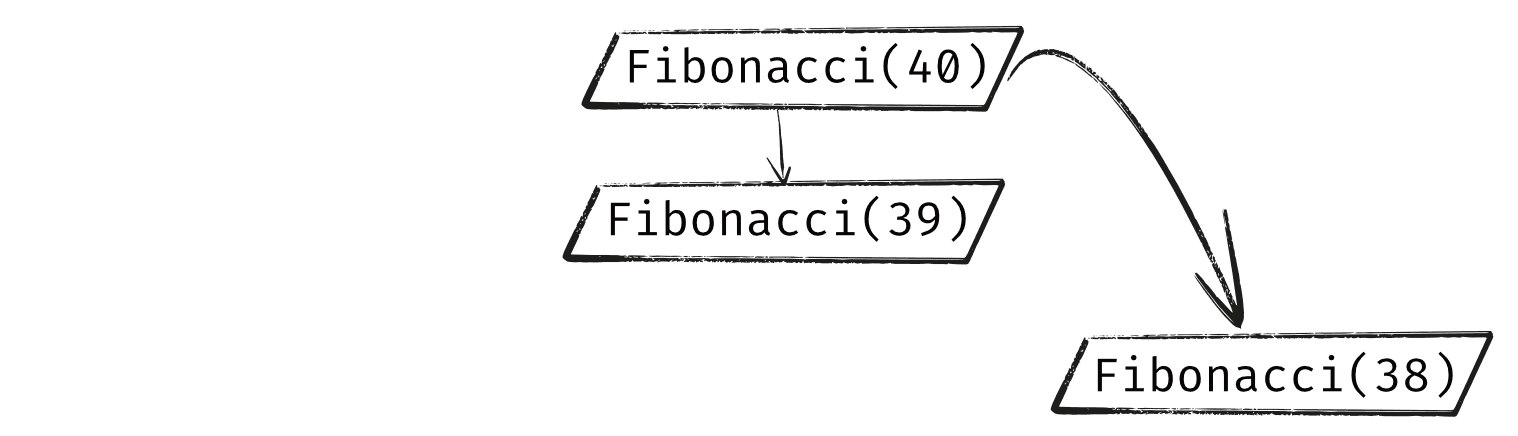
However, the Fibonacci(39) branch is also going to call Fibonacci(38). Because of this, we now have two duplicate branches that are each independently doing exactly the same thing.

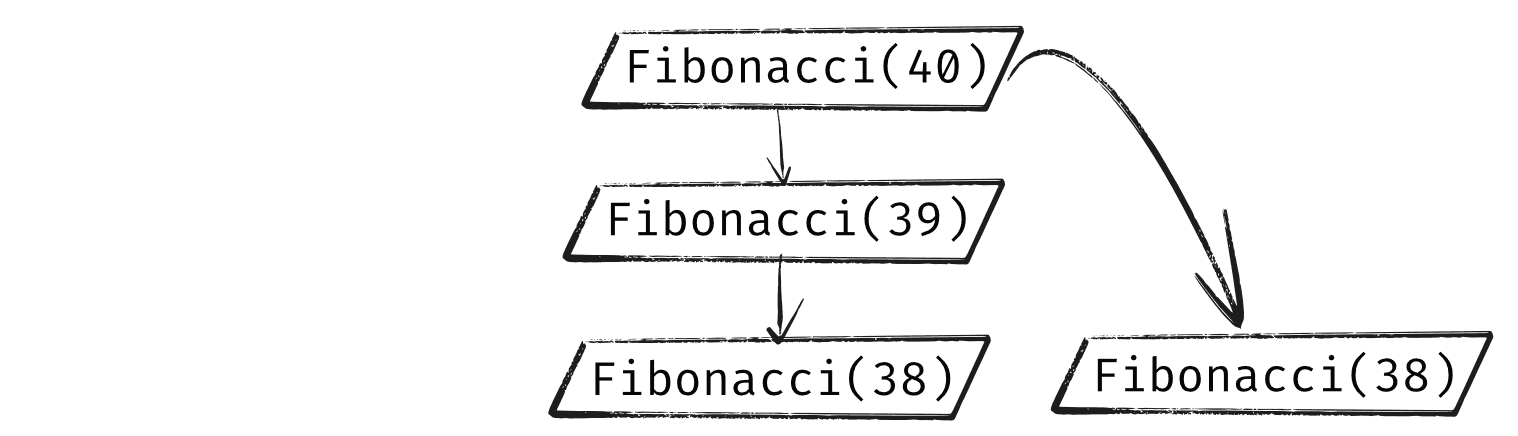
The Fibonacci(39) branch and both Fibonacci(38) branches will call Fibonacci(37), so we will have three of those:

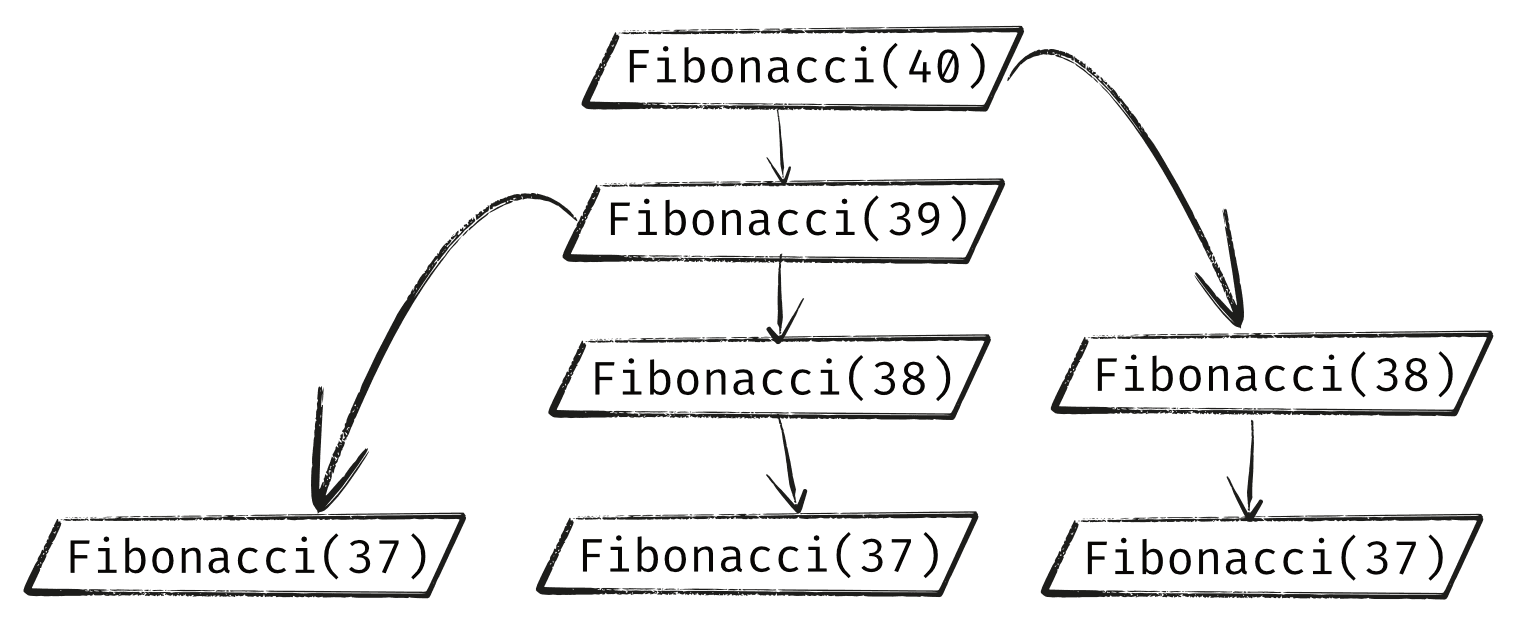
This wasteful duplication compounds as we move further down the tree. The two Fibonacci(38) branches and the three Fibonacci(37) branches will all call Fibonacci(36) so we now have 5 separate branches doing the same calculation.

By the time we reach Fibonacci(20) we will have 10,946 branches doing the same calculation.

By Fibonacci(10), we have over a million branches. And, as we saw from our code example, each of those Fibonacci(10) branches requires 109 calls to determine the 10th Fibonacci number - over 100 million function calls just in that part of the tree.

Caching and Memoization

So, we have a performance problem caused by massive duplication of the same work. How do we solve this problem? Caching is the process of saving data we previously calculated, so we don’t need to calculate it again.

Memoization is a specific form of caching, where we cache the result of a function call for a given set of arguments. So, before the function returns the result, it stores the result in the cache.

Then, in the future, if the function is called again with those same arguments, we can get the return value from the cache, rather than recalculate it.

Typically, hashmaps such as a std::unordered_map are used for this cache.

Hash Maps using std::unordered_map

Creating hash maps using the standard library's std::unordered_map container

We use a map below and update our recursive function to make use of it. If our Fibonacci() function is called with a number it has already calculated, that number will be in the Cache map, so we can return it from there rather than recalculating it:

1#include <iostream>
2#include <unordered_map>
3
4int Calls{0};
5std::unordered_map<int, int> Cache;
6
7int Fibonacci(int n){
8  ++Calls;
9  if (n == 1) return 1;
10  if (n == 2) return 1;
11  if (Cache.contains(n)) return Cache[n];
12  Cache[n] = Fibonacci(n - 1) +
13    Fibonacci(n - 2);
14  return Cache[n];
15}
16
17int main(){
18  std::cout << Fibonacci(10)
19    << " (" << Calls << " calls)";
20}

Now, our calculation of the 10th Fibonacci number only takes 17 calls, rather than 109.

155 (17 calls)

Finding the 40th number is now noticeably faster, as it takes only 77 calls, down from 205 million. We’ve moved from an algorithm that scales exponentially ($O(2^n)$) to one that scales linearly ($O(n)$)

Cache Keys

We’ve seen that caches are essentially key-value pairs. The key is the input to a function (or some process), whilst the value is the output that the process produces.

In the Fibonacci example, the input to our function was simple - a single, integer argument. The return value of Fibonacci(40) is stored in our cache with a key of 40.

But things are not always that simple, so we sometimes need to dedicate some thought to how we create our keys.

For example, what if our function had two arguments? What key would we use to store a function call with the arguments (12, 3)?

We could add them, such that our key would be 15. But (10, 5) would also have a cache key of 15. For our hypothetical function, are these argument lists equivalent? If so, our key strategy is suitable, but if not, it will cause bugs.

Another strategy might be concatenating the arguments, such that the key is 123. But then that would mean (12, 3) and (1, 23) would be treated as equivalent.

Another more robust strategy is to concatenate them, with a separator between arguments, such as a comma. For example, our key for the function call (12, 3) could be the string "12,3". whilst (1, 23) would be "1,23"

This is a very common technique, but even this is not a universal solution. For example, it will not work if our arguments are strings, which may include their own commas. And our arguments may not be easily convertible to strings - they may be complex objects from a custom class.

The key point here is that we need to be considerate in how we generate cache keys, and there is no universal strategy. We need to adapt our technique to our specific function.

Side Effects and Pure Functions

There are other considerations we have to be aware of when dealing with memoization. The first is around side effects. A side effect is anything a function does, besides returning a value. It can include calling other functions, updating the values of variables in the parent scope, freeing memory, and more.

In the following example, our function has the side effect of logging into the console. But, whether that happens depends on whether or not we had a cache hit or miss.

1int Square(int x){
2  if (Cache.contains(x)) return Cache[x];
3  std::cout << "Squaring!"; // Side effect
4  return x * x;
5}

A function whose observable behavior changes depending on whether or not something is cached is generally a red flag and should prompt us to reconsider our implementation.

Another aspect to consider is that a function’s return value does not necessarily depend on just its arguments. It can also access values from other locations, such as parent scopes or calls to other functions.

The following function will return the wrong value if it encounters a cache hit, but the Multiplier variable in the parent scope has changed since that entry was added to the cache.

1int Multiplier { 5 };
2int Multiply(int x){
3  if (Cache.contains(x)) return Cache[x];
4  return x * Multiplier;
5}

When we decide to memorize a function, we need to consider these possibilities and mitigate them. Even better, we can create functions that don’t have side effects and whose output depends only on its inputs, rather than some external state.

A function that does not have any observable side effects, and always returns the same output for a given set of arguments, is called a pure function.

Beyond being easier to memoize, they also tend to be easier to test, and easier to debug. So, when given the opportunity, we should generally prefer to make our functions pure.

Summary

In this lesson, we explored recursion, and how it can solve problems by breaking them down into simpler versions of themselves. The main points we covered include:

• Recursion is a technique where a function calls itself to solve problems that can be divided into similar, smaller problems.
• Recursive functions typically consist of a base case to terminate the recursion and a recursive case that moves towards the base case.
• The Fibonacci sequence serves as a classic example to demonstrate how recursion can be applied to solve problems.
• Recursive functions can lead to performance issues due to the exponential increase in function calls, as illustrated by the naive Fibonacci implementation.
• Memoization is a form of caching that stores the results of expensive function calls, preventing redundant calculations.
• Implementing memoization in recursive functions, such as the Fibonacci example, can transition an algorithm from exponential time complexity to linear time complexity, drastically improving performance.
• Designing cache keys requires careful consideration to ensure that memoization works correctly, especially when functions take multiple arguments or complex data types.
• Pure functions, which have no side effects and return consistent outputs for the same inputs, are ideal for memoization as they simplify caching logic and reduce the risk of errors.

Next Lesson

Variadic Functions

An introduction to variadic functions, which allow us to pass a variable quantity of arguments

ContinueView Course